There are two ways for how data can be migrated from Project Online to Planner Premium (Project for the web):
- using Microsoft MPP import feature;
- using FluentPro Project Migrator.
While Microsoft Provides the MMPP import feature, there is a large number of associated limitations and data quality issues with the MPP import feature that are solved by FluentPro Project Migrator.
Please review the detailed overview of data migration elements that are supported by FluentPro Project Migrator only or that can be transferred more accurately using Project Migrator vs Microsoft MPP import feature.
1. Project Migrator is more accurate with the ‘Fixed Duration’ project schedule mode which is recommended to keep for the initial project migration.
2. Migrating Multiple Projects
Using Project Migrator, you can migrate either all or selected projects in bulk. Using the MPP import feature you need to open each project in Project Pro, save it as .mpp file, and then import it to Planner Premium one by one.
3. Support of Office 365 Groups
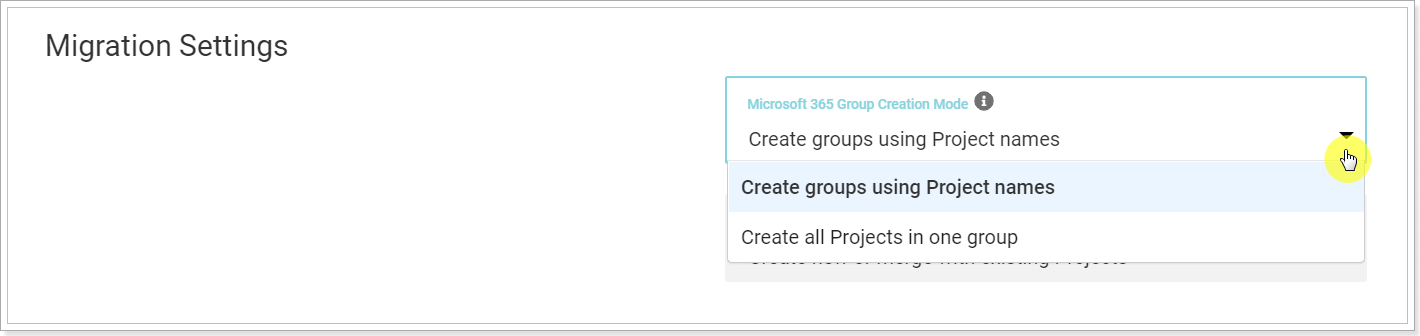
Using Project Migrator, projects will be migrated to the required Office 365 group: you can select either to create a new group for each project or create all/several projects in one group. Using the Microsoft MPP import feature all projects will be imported without any groups.
After migration using MPP Import:
After migration using Project Migrator:
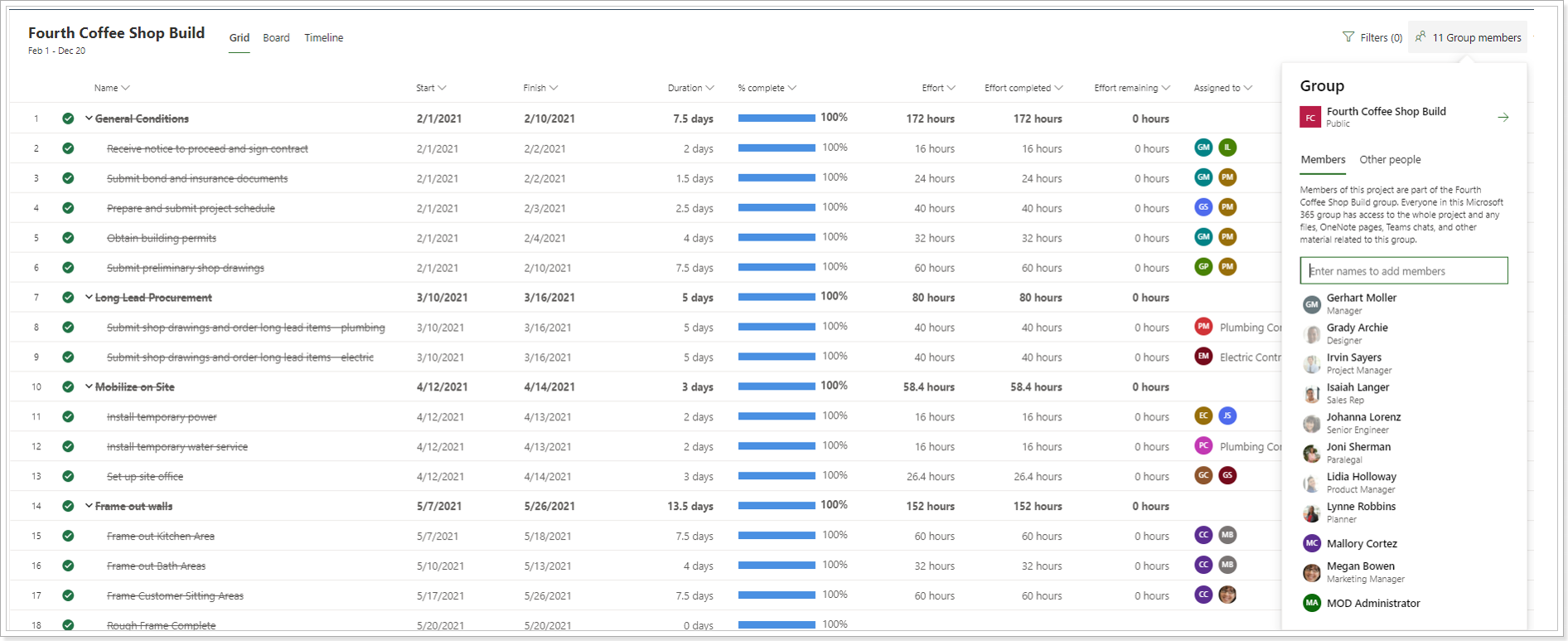
4. Resource Migration and Mapping
Using Project Migrator you can migrate all project team members and task assignments whatever type they are – either enterprise resources or just local resources.
All you need is to map source users/resources with target users/resources in user mapping section.
Please note: The users cannot be migrated from the source Project Online PWA to the target Planner Premium tenant. User accounts should already exist on the target environment (in the Active directory of your Planner Premium tenant) before the migration starts. In this case, Project Migrator will find the required users by their accounts and will map them automatically to migrate the assignments and other resources data to the target Planner Premium environment.
Once user mapping is performed all team members and assignments will be migrated in the following way:
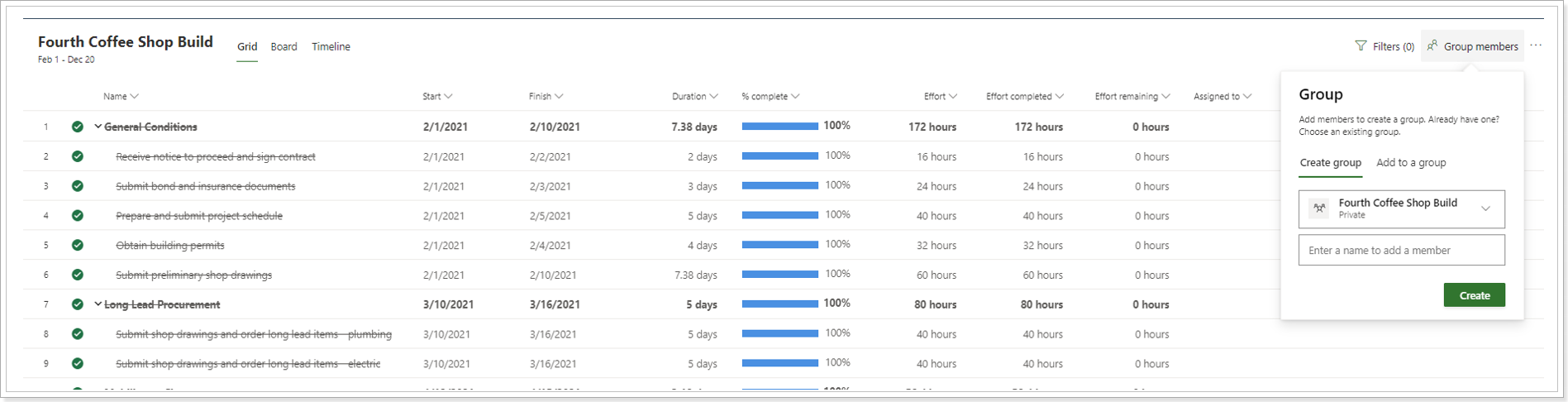
- All source project team members will be added to the corresponding Office 365 group as members (if they are mapped with existing Office 365 users on the target system).
- All source tasks assignments will be also migrated as assignments to the target if user mapping is performed.
- If a source assignment is mapped with an existing Office 365 target user, it will be added to the corresponding Office 365 group as a member and an assignment will be added to the task. Also, it will be added to target project team and corresponding bookable resource will be created if it does not exist already.
- To preserve all task assignments, even if there are local resources in the source projects as assignments they also will be migrated as local resources to the target project.
- Also, in Project Migrator you can select the 'Create resources for not mapped users' option that allows creating bookable resources in the target Planner Premium system and preserving the task assignments for users that were not mapped. However, users (new user accounts) will not be created in the Entra ID (formerly Azure AD) on the target.
Using MPP import all tasks will be imported without assignments.
Source Data:

After migration using MPP Import:
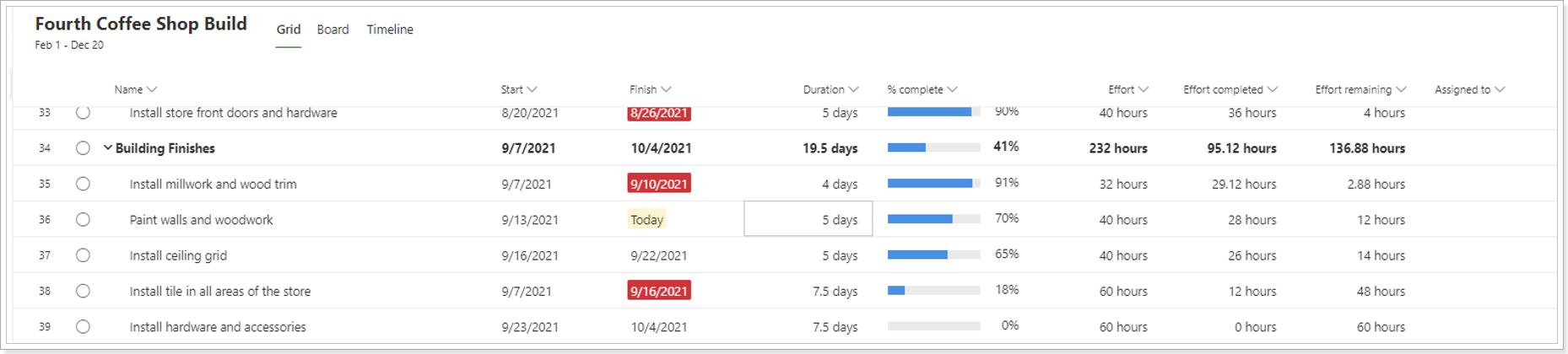
After migration using Project Migrator:
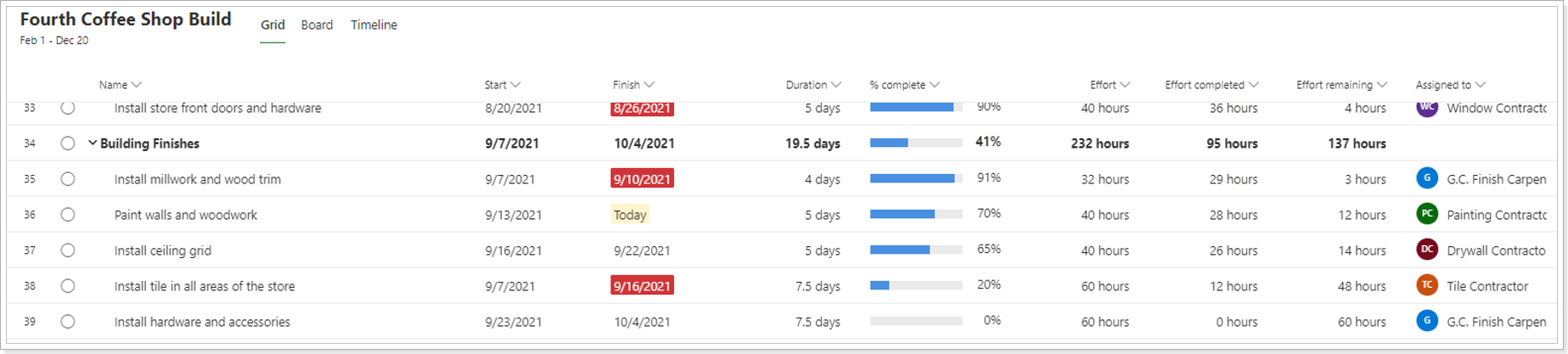
5. More accurate migration for manual tasks
Tasks will be migrated more accurately with Project Migrator. When importing all manual tasks are recalculated automatically.
Source project:
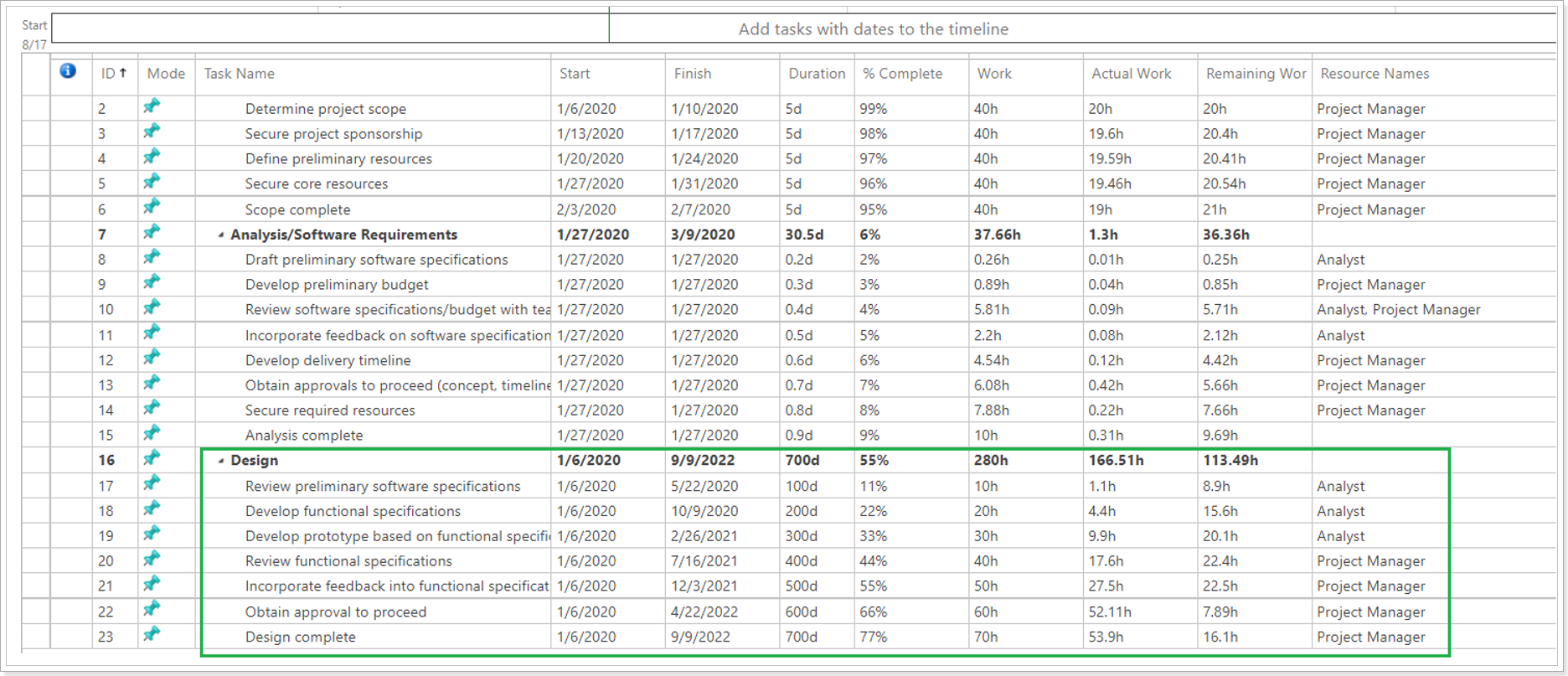
After migration using MPP Import:
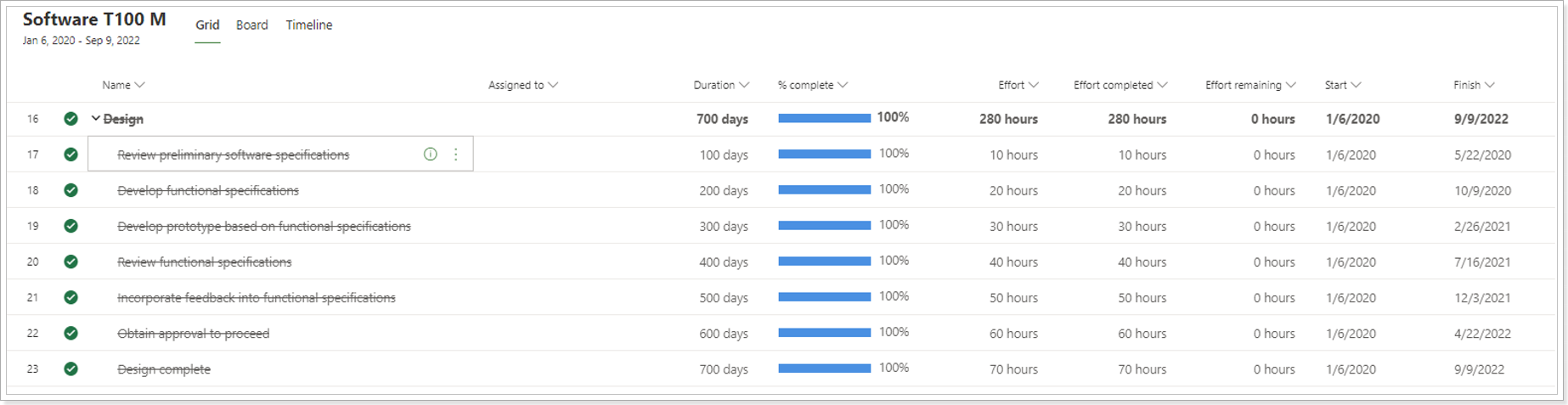
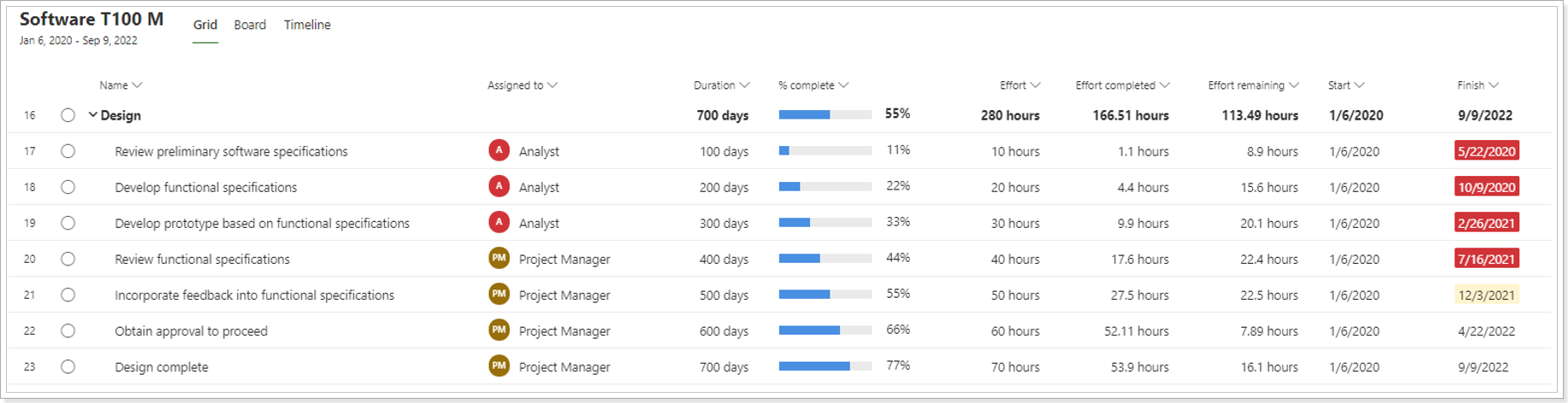
After migration using Project Migrator:
Source Data:
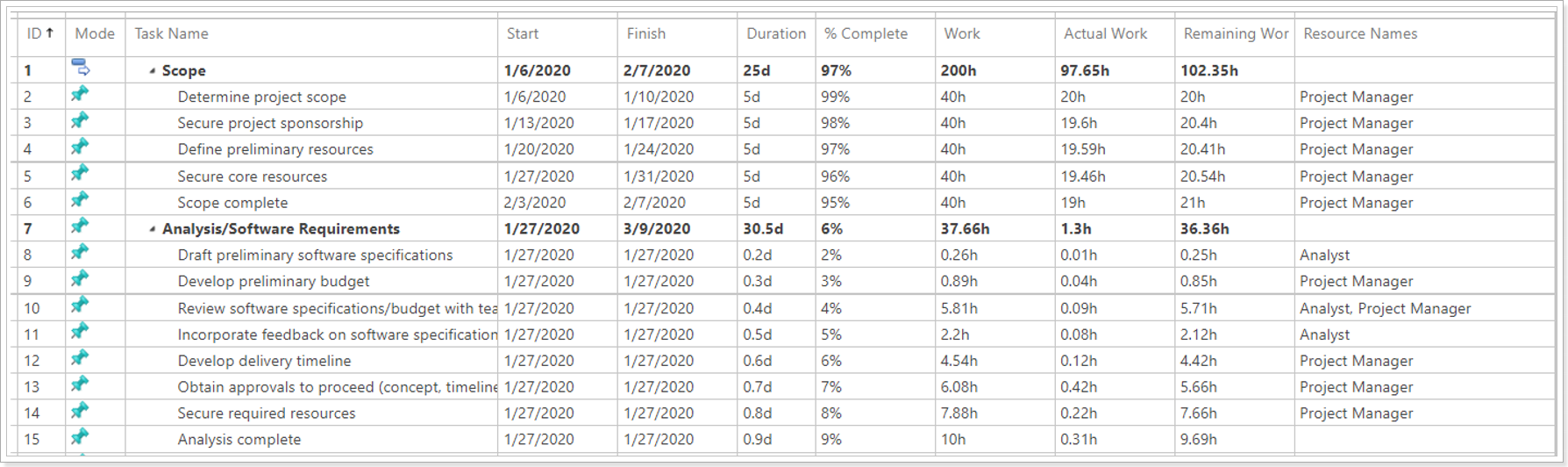
After migration using MPP Import:
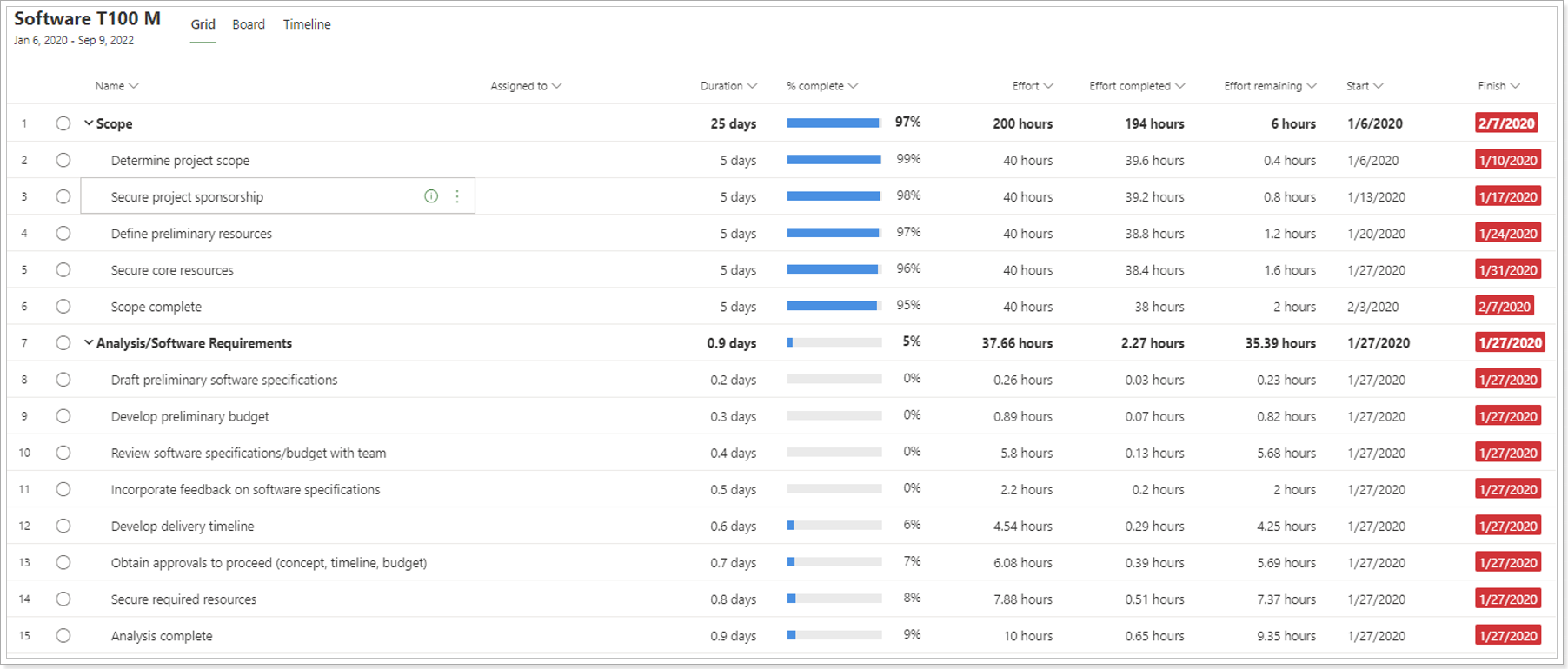
After migration using Project Migrator:
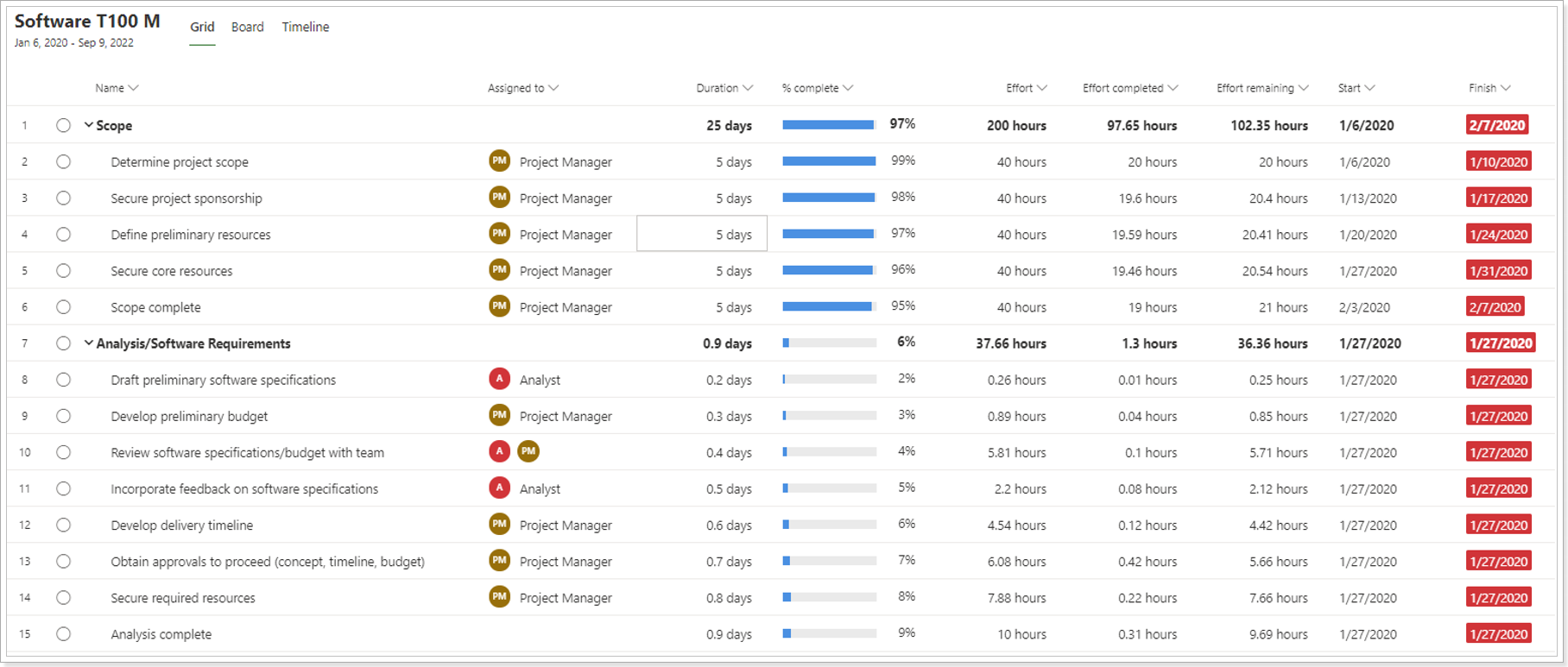
6. Task Fields Mapping
Project Migrator provides more flexibility allowing to change task fields mapping, e.g., you can migrate text from any custom task field of the text type to the target task 'Notes' field just by selecting this field in the task mapping section:
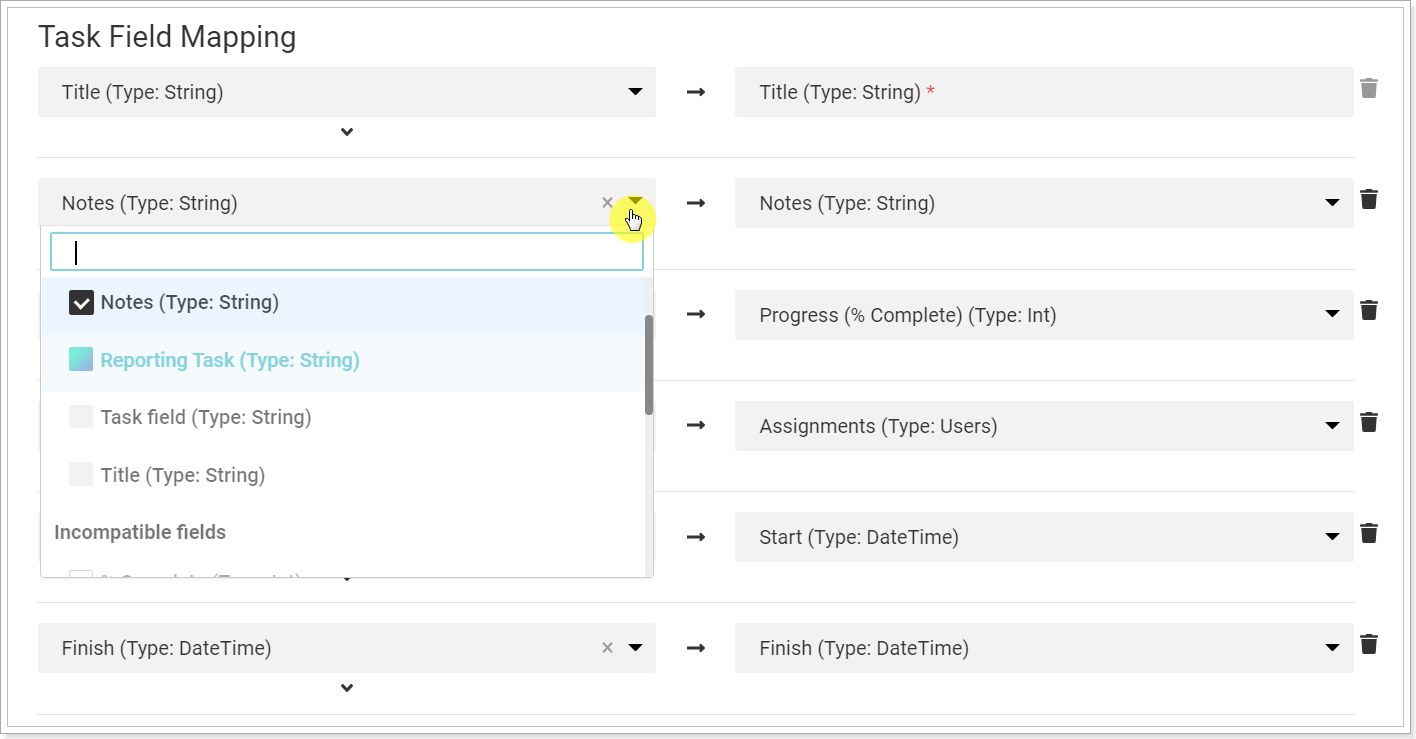
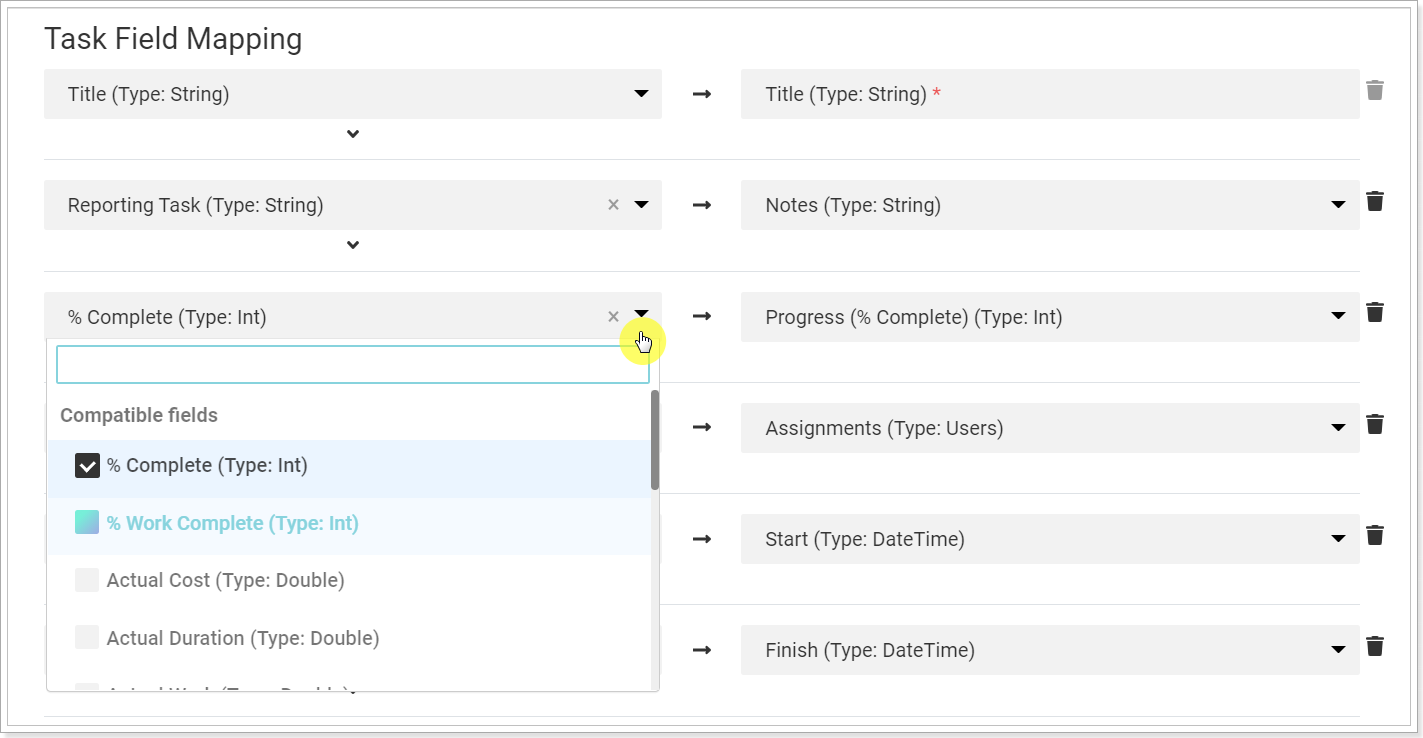
If you want to migrate % Work complete to the task progress instead of default % Complete, all you need is to remap the required fields:
7. Support of Target Calendar Time Zones
More accurate handling of dates in different time zones. E.g., the Target Calendar Template is in GMT+2 time zone.
Source Data:

After migration using MPP Import:
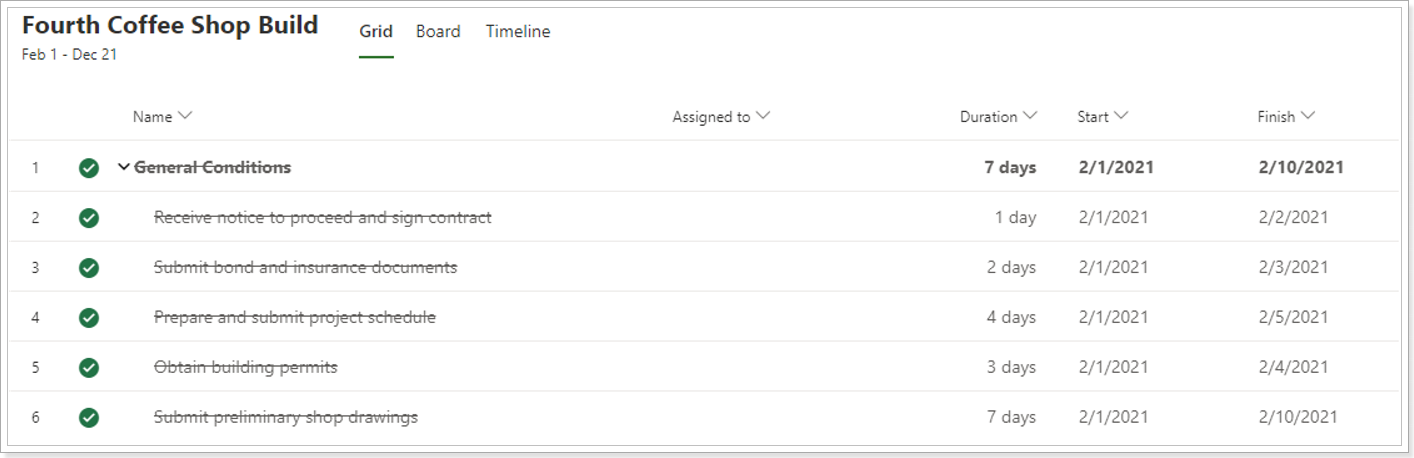
After migration using Project Migrator:
8. Project Calendar Mapping
If the source project is based on a custom calendar and there is the same calendar with the same name on the target system Project Migrator will find and match the calendars. As a result, source data will be transferred more accurately, such project will be migrated also based on the custom calendar.
9. Working around Planner Premium Limitations
Using Project Migrator, you can migrate all projects even if they are not supported in Planner Premium data. Using Microsoft MPP import you will need to edit your project to remove such data and then perform import again.
Planner Premium migration limitations with MPP import that are solved by FluentPro Project Migrator:
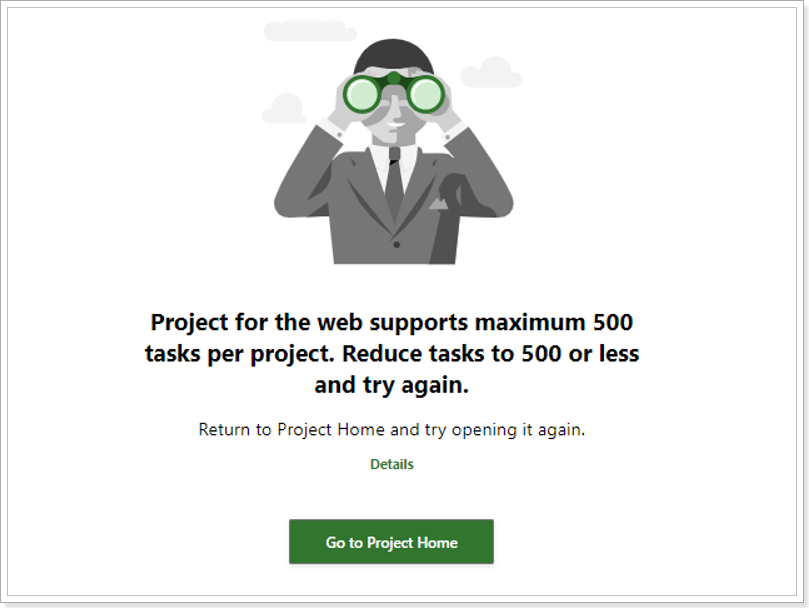
1) If the project has more than 1000 tasks Project Migrator will migrate this project successfully migrating the first 1000 tasks and skipping others. It is not possible to import such a project using MPP import, you will need to edit data in the project first and then perform import again.
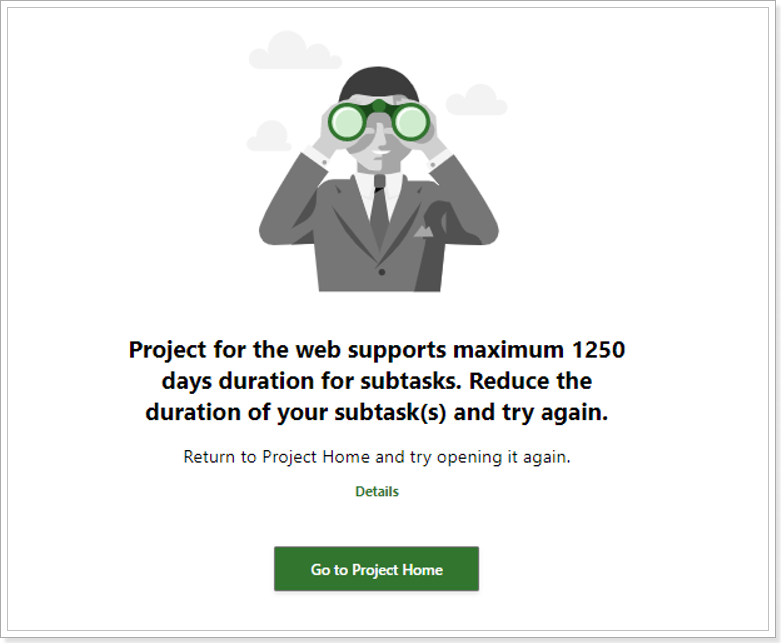
2) If there are tasks with a duration >1250 days in the project, Project Migrator will migrate this project successfully just setting a 1-day duration for tasks out of possible range. It is not possible to import such a project using MPP import, you will need to edit data in the project first and then perform import again.
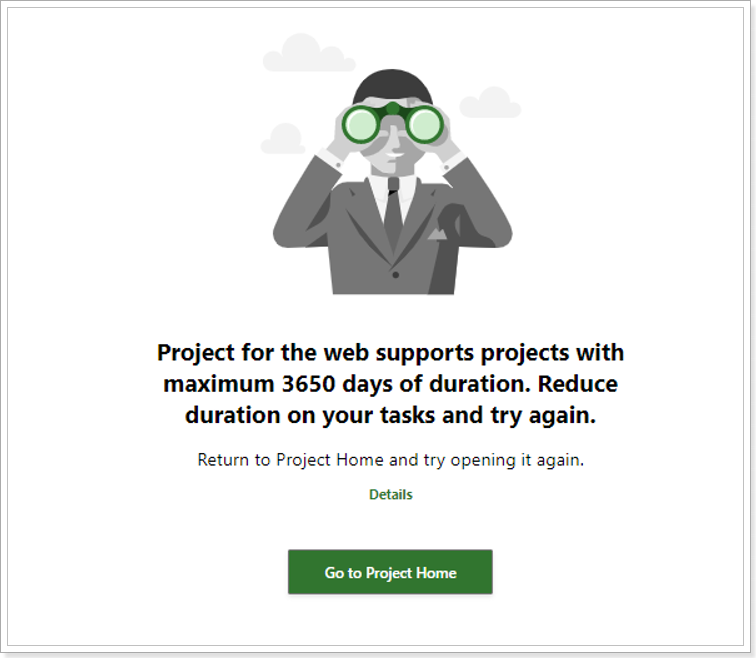
3) If the project range exceeds 3650 days Project Migrator will migrate this project successfully just not setting dates for tasks that are out of possible project range. It is not possible to import such a project using MPP import, you will need to edit data in the project first and then perform import again.
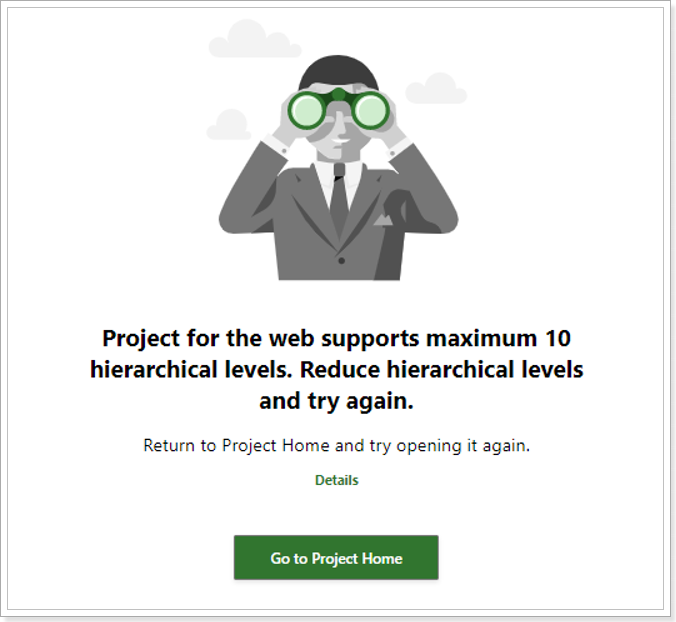
4) If the source project has more than 10 hierarchical levels Project Migrator will migrate this project successfully just moving such tasks to the last possible outline level. It is not possible to import such a project using MPP import, you will need to edit data in the project first and then perform import again.